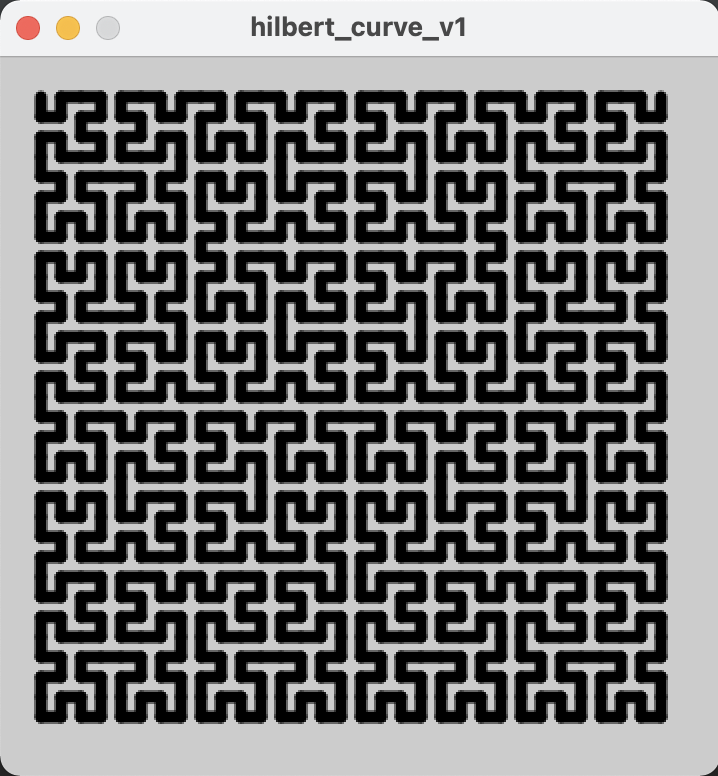
I heard about Hilbert curves a while ago and thought they sounded fun!

I had a play, trying to understand the algorithm from Wikipedia, but I got tired of that pretty quickly and stumbled across this blog post.

http://blog.marcinchwedczuk.pl/iterative-algorithm-for-drawing-hilbert-curve

It gave me a very neat iterative algorithm that could find the coordinates for a single point on the "curve".

The blog post was written in JavaScript. I tried converting it to Python but the support for Python in Processing is rather lacking, so I decided to use Java even though I am less familiar with it. This actually made it easy to convert the code in the blog post, as the syntax is quite similar, but it's going to make further development of this project a bit more challenging.

My code has 3 parameters that you can tweak, which affect the number of iterations of the curve (log_2(N)), the size of the curve, and the amount of space around the edges

int N = 32;
int SCALE_FACTOR = 10;
int PADDING = 2;

The main algorithm looks like this

int[] hindex2xy(int hindex, int N) {
  int[] tmp = POSITIONS[last2bits(hindex)];

  hindex = hindex >> 2;

  int x = tmp[0];
  int y = tmp[1];

  for (var n = 4; n <= N; n*= 2) {
    var n2 = n / 2;

    switch(last2bits(hindex)) {
      case 0: /* case A: left-bottom */
            int tmp2 = x; x = y; y = tmp2;
            break;

        case 1: /* case B: left-upper */
            y = y + n2;
            break;

        case 2: /* case C: right-upper */
            x = x + n2;
            y = y + n2;
            break;

        case 3: /* case D: right-bottom */
            int tmp3 = y;
            y = (n2-1) - x;
            x = (n2-1) - tmp3;
            x = x + n2;
            break;
    }

    hindex = hindex >> 2;
  }

  int[] out = {x, y};
  return out;
}

And the rest of the code is just Processing stuff, to take my list of points and draw them out into this beautiful pattern

Check out the source code on my GitHub

https://github.com/adnathanail/hilbert-curve