How many puzzle pieces are there?
Alex
—Jan 08, 2025
We picked at a mathematical thread and unravelled a whole jumper
Introduction
Just before new year I started a rather tricky, but rather beautiful, puzzle of a map of the lake district with a friend. A week or so later I finished it with 2 friends P and C.
It was about 01:30 by this point, we'd been going since about 20:00, so a sensible person would have gone to bed. Unfortunately, P turned to me and asked
"How many possible puzzle pieces are there?"
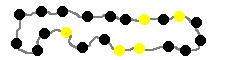
We quickly defined that they weren't interested in corner or edge pieces, and were assuming each piece had exactly four sides, and each side had either an in or an out.
P's first thought was combinatorics, and said it was something like or .
I said it definitely wasn't that, it was , because you have 4 sides, each with 2 possible states. But it wasn't that either.
C pointed out that I'd forgotten about rotational symmetry, and that a piece could only have 0, 1, 2, 3, or 4 outs and therefore the answer was .
But a quick scribble determined that the case with 2 outs had 2 options that couldn't be rotated to each other, so the answer was !

That could have been the end of it, but P then had to ask
"Why?"
Was it ? That's a neat-ish sum, maybe its ?
Other cases
We needed to work out some other cases (ignoring the fact that you can't tessellate 2D shapes which aren't triangles, squares, or hexagons).


By hand, we calculated cases (and got it right for ) (where is the number of sides the shape has).
Letting be a function which gives the number of arrangements of ins and outs, unique under rotation, of an -sided shape, we found:
It's not .
But there's something vaguely approaching a pattern here, which is that the differences between each term is ; not quite enough information to determine anything yet though.
At this point it was at least clear that the first stage of the calculation was to work out sub-cases, which are the number of outs (or ins, it doesn't matter) from to .
So can we see any patterns if we break it down like this? Let be the number of rotationally unique arrangements of outs of an -sided shape
It's looking a bit neater!
Firstly, we can see that each line is symmetrical, i.e. the first and last items the same, second and second to last, etc.
Lemma 1
When we have no outs and all outs, any puzzle piece with any number of sides will be entirely rotatable because none of the sides are distinguishable.
Lemma 2
Similarly, when we have 1 out and all-but-one outs (which is the same as just 1 in), all pieces can be rotated onto each other.
Lemma 3
There seems to be some structure to the middle terms, but I think we need more cases; it's time to bust out some Python.
Scripting
We can model a possible arrangement as a binary string. E.g. a 4-sided piece with all ins would be , and one arrangement of a 6-sided piece with 3 outs would be .
For our purposes, that 6-sided shape is also equally validly represented as , , , , and .
Initially I took a given and , and generated a base string; e.g. for the string would be .
I then found all the permutations of the string.
This worked, but it was very slow, as it sees each character in the string as unique and therefore tries all 3 s in the first spot, and then the second, etc., when they are actually identical.
Interpreting the strings as binary, we can just count , , etc. and find all the strings with 3 s.
To easily determine when we have duplicate strings, it's helpful to have a consistent normalisation function, so any given shape has a unique "authoritative representation". Again interpreting the strings as binary, we can define that the string that encodes the smallest binary number is the normalised one.
Putting this together I produced the following script:
V1 couldn't get past about 11 sides without taking far too long, but, thanks to the optimisations from the insights above, V2 can easily reach 20 sides in about 10 seconds.
This produced the following output
1 1 # 1 sides 2 combinations
1 1 1 # 2 sides 3 combinations
1 1 1 1 # 3 sides 4 combinations
1 1 2 1 1 # 4 sides 6 combinations
1 1 2 2 1 1 # 5 sides 8 combinations
1 1 3 4 3 1 1 # 6 sides 14 combinations
1 1 3 5 5 3 1 1 # 7 sides 20 combinations
1 1 4 7 10 7 4 1 1 # 8 sides 36 combinations
1 1 4 10 14 14 10 4 1 1 # 9 sides 60 combinations
1 1 5 12 22 26 22 12 5 1 1 # 10 sides 108 combinations
1 1 5 15 30 42 42 30 15 5 1 1 # 11 sides 188 combinations
1 1 6 19 43 66 80 66 43 19 6 1 1 # 12 sides 352 combinations
1 1 6 22 55 99 132 132 99 55 22 6 1 1 # 13 sides 632 combinations
1 1 7 26 73 143 217 246 217 143 73 26 7 1 1 # 14 sides 1182 combinations
1 1 7 31 91 201 335 429 429 335 201 91 31 7 1 1 # 15 sides 2192 combinations
1 1 8 35 116 273 504 715 810 715 504 273 116 35 8 1 1 # 16 sides 4116 combinations
1 1 8 40 140 364 728 1144 1430 1430 1144 728 364 140 40 8 1 1 # 17 sides 7712 combinations
1 1 9 46 172 476 1038 1768 2438 2704 2438 1768 1038 476 172 46 9 1 1 # 18 sides 14602 combinations
1 1 9 51 204 612 1428 2652 3978 4862 4862 3978 2652 1428 612 204 51 9 1 1 # 19 sides 27596 combinations
1 1 10 57 245 776 1944 3876 6310 8398 9252 8398 6310 3876 1944 776 245 57 10 1 1 # 20 sides 52488 combinationsNow we can clearly see that the third items (and third to last), form a pattern of numbers increasing by 1 for every 2 increases of .
So when the third value is 2, when the third value is 7.
Lemma 4
Lost in the fourth item
The next pattern is a little less clear, but if we look at the differences between the values for the fourth item (starting with 8 sides, as I'm not certain that the third value being across the center line won't break things), there is something there.
7 10 12 15 19 22 26 31 35 40 46 51 57
3 2 3 4 3 4 5 4 5 6 5 6
- + + - + + - + + - +But, to my knowledge, that's not a simple polynomial of the form , because of the repeating nature of the 2nd order (and all higher) nth term(s).
Entering that sequence in the OEIS () gives 3 results:
- Maximal number of points that can be placed on a triangular grid of side n so that there is no pair of adjacent points.
Both of the first sequences are identical except the second has an extra at the start, and they also match the earlier terms of the sequence which I ignored in case they messed up the results ().
All 3 sequences are identical from onwards.
Entering the fifth term into the OEIS, starting from to avoid the centering issue (), gives just 1 result:
- Molien series of 4-dimensional representation of cyclic group of order 4 over GF(2) (not Cohen-Macaulay).
This result also matches the first 6 items which I omitted.
The comments on this series include
"a(n) is the number of necklaces with 4 black beads and n white beads."
Why is it talking about necklaces?
Necklace numbers
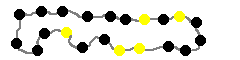
The mathematical study of necklaces looks at how many ways there are to order different coloured beads on a string. If we imagine a four-sided puzzle piece with in, out, in, out this is equivalent to a 2-coloured necklace with four beads: white, black, white, black.
Our representation of puzzle pieces as binary strings is the exact same representation used in the study of necklaces. We take a 2D object, whose relevant properties are held in a rotatable ordered list, and represent it as a string of characters.
Formally
"An-ary necklace of lengthis a string ofcharacters, each ofpossible types. Rotation is ignored, in the sense thatis equivalent tofor any."
There are 2 types of necklace: fixed, and free.
For free necklaces, mirror images are seen as equivalent, so and would be equivalent.
For a fixed necklace, we imagine it laid on a table, able to be rotated, but not flipped over (it may not be taken "out of the plane").
In our case, if you flip over a puzzle piece it has nothing on the other side, so our necklaces must be fixed.
It's a bit easier to visualise a necklace with 6 beads, than a theoretical 6-sided puzzle piece, so I was able to create a simulator where you can enter a bit-string and see the corresponding necklace. I also added some functionality to demonstrate how rotation works on bit-strings.
If you click the Shunt button (without clicking Unfold) it is evidently the same necklace/puzzle piece. If you then click Unfold and Shunt you can see the same operation occurring. Moving a bit from the start to the end of the string still represents the same puzzle piece.
The bit-string starts from the red outlined circle
Lots of maths
Now we have a foothold in established maths, we can work towards a better formula for
Definitions
We need to do some organisation, and give some things names.
Let be our set of rotation operations
For each bit string let's consider the operations that have no effect on it
| x | 90° | 180° | 270° | 360° |
| 0000 | ✅ | ✅ | ✅ | ✅ |
| 0001 | ✅ | |||
| 0010 | ✅ | |||
| 0011 | ✅ | |||
| 0100 | ✅ | |||
| 0101 | ✅ | ✅ | ||
| 0110 | ✅ | |||
| 0111 | ✅ | |||
| 1000 | ✅ | |||
| 1001 | ✅ | |||
| 1010 | ✅ | ✅ | ||
| 1011 | ✅ | |||
| 1100 | ✅ | |||
| 1101 | ✅ | |||
| 1110 | ✅ | |||
| 1111 | ✅ | ✅ | ✅ | ✅ |
For a given , we call the set of operations that have no effect on it the stabilizer
E.g.
We can also group our bitstrings, into ones which can be transformed into each other by our rotation operations
For a given , we call the set of other bitstrings into which it can be transformed the orbit
E.g.
Orbit-stabilizer Theorem
For a given , if two operations give the same result ( e.g. ) then the difference between those two operations must have no effect on .
I.e. the difference between those two operations must be in the stabilizer of
What is the ∘ symbol?
The ∘ symbol means function composition, AKA the effect of applying 1 function then the other. For example 180° ∘ 90° means rotate 90 degrees then rotate 180 degrees, which is equivalent to the single function rotating 270 degrees.
E.g.
Composing rotations
-270° ∘ 90° = -180° which is the same operation as 180°, just a different notation
So, for a given , we can split our set of operations into "equivalence" classes
E.g. for we have 2 classes (with 2 operations per class):
Whereas for we have 4 classes (with 1 operations per class):
Each equivalence class maps to an element of the orbit. One of the equivalence classes will be the stabilizer. All the equivalence classes are the same size.
Therefore, for a given , we can say that the number of bit strings it's possible to rotate it to (orbit), multiplied by the number of operations which have no effect on it (stabilizer), gives the total number of operations.
This is the Orbit-stabilizer Theorem!
Further reading:
Burnside's Lemma
Let's now consider the sum of the size of the stabilizers for all our bitstrings .
Using the Orbit-stabilizer Theorem above, we can write this as:
For a given orbit , each will contribute to the sum, and there are exactly elements in , so each orbit contributes to the sum.
So
Where is the number of orbits of under (AKA the number of sets of bitstrings that can be rotated onto each other AKA the number of unique puzzle pieces!)
Rearranging this we find
A formula for the number of unique puzzle pieces!
This is Burnside's Lemma!
Further reading:
Restructuring Burnside's Lemma
To make it easier to use in the next section, we need 1 more definition in order to restructure Burnside's Lemma into something more usable.
For an operation , a fixed point of is an element such that
E.g.
So for the operation , is a fixed point
The set of all fixed points of with respect to is often denoted
The sum of the sizes of the sets of all fixed points of for each operation is the same as the sum of the sizes of the sets of the stabilizers for each item
Proof
So we can restate Burnside's Lemma as
Where
is the number of orbits of(number of unique puzzle pieces)is the number of operations we have (in our case 4: 90°, 180°, 270°, 360°), andis the number of bitstrings unchanged under a given operation
The General necklace polynomial
We've got a formula, but we've lost all the variables we knew.
How do we get this in terms of ?
Here's some easy wins:
is equivalent to ouris the size of the set of operations, in the square puzzle-piece case we have been considering this is, in general for an-sided puzzle piece there arepossible rotations. So
We originally defined our set of operations as rotations .
This intuitively maps onto puzzle pieces.
This same "rotation" is equivalent to moving a certain number of bits.
E.g. the operation is the same as moving 2 bits from the start to the end.
So, without changing its meaning, we can also define as
For a string we can define its period.
This is the length of its largest repeating pattern.
E.g. the period of is 2, because repeats twice. The period of is 4, and the period of is 1.
For a given bitstring to be unchanged over a rotation , its period must be divisible by , otherwise the rotation will cut the repeating string somewhere in the middle of its pattern.
Also, its period must be divisible by the length of the string, otherwise it's not possible for it to be a repeating pattern.
If we have a period of 3, with the periodic substring being , we couldn't then have a full string of length 5 because the last would be cut off.
Therefore, the largest possible period for a string of length , and a rotation , can be found by the greatest common divisor of and .
E.g. for and the largest possible period is .
Any repeating 2-element substring will be unchanged by a rotation of 2.
, , but
Now we know the maximum period of our substring for a given , we can find how many there are using the approach I suggested right back at the start.
The number of possible 2-bit strings of length is
Putting this into Burnside's Lemma gives us
This is (almost) the General necklace polynomial!
General necklace polynomial
The general necklace polynomial works for any number of colours of bead, not just 2, so we replace the 2 with a:
Further reading:
Grand finale
I implemented this formula in Python, and the results agree with our earlier calculations!
This version can calculate the first 10,000 items in 12 seconds!
How many 10,000-sided puzzle pieces are there you ask?
39897272610354132284446398613810320644405496088115 03759328085091196768089235465779806011735633675552 02466375950869095575873542472741001522199655753066 61981717539706122975291524378055297002419549086191 55468091853123189402751848436093492465726645260451 57294068489911193959436721484863944971692308820256 22213909059287359012980795440199234047501695567519 57143148840241903962171159036242821424875840711165 67470882091180159972219597251000256395652863260341 84654585672731788027482612208717928878980735229395 65598096123542766957820624219176921943727102938842 86816919054152294515586458043487280364974661125915 70510792152253950883425848174720766478953758539617 38714953117092042363028797665898168037338340926480 63054323130351792853198593574454035824810605785914 18460651647129897425121472371986393860875898130670 34964665054680995932660432414457805387723796432664 08138215920693056996522142696014464829921066526166 53527576754345377153967735370552870446988331290712 19078929391516030131166998221461425247857505460467 60348973222828114033834577726969664122483513106817 22312865391904774937315214803273194373788688688543 22528429796447054025521987913842603230778570499144 64773188507437327704780017368460299508807647899642 02379515821739442793396336421644401110233523962749 21464675991278818880284293055345123882574366602860 54960143299619556007689856183064412755980084594104 29769589994298747506291466015163715276396331907054 10867779338681305677296191301550839547361905543866 79598058269229545356259281959758329316174192784967 72217421479359013750106539893983298267169964517424 16887638960478866013254477866634076865200107152727 58959931971262550661880500755343749282091892269328 03448756281640838117894186206158332024196662002492 06840724719351861976831472688159907948950731218774 87915250104489194517708456935730991918924643884335 97795172325602747156659785251284037406244297627497 41332983363289691428392332013667341056976137510929 07606989824270444328543816007673640181846617227402 19824526248176538400707604750277785675229749507124 27039489394771932958523767672590716963957989391737 08277611319434111776991279972296303737420217915933 23940232729514855261385464268846599095512559512500 22897532284065237415574772819744124432030786464306 18321277236629994524554800065147960831223509872948 93072278111152659136683618959641139165804488755720 17109792610216027671122272390339819207722629347289 33553954530310349679814445922175654269701404536556 56374905737257153466636532656043230349588355036558 58864101183881457210625409063716000928822177609390 69593204676317093982906706951084096235263717103721 98952818749062061911053554230284722774695643316742 25101893603353870375434770025506117048949110908442 88582512891860924242126165367345859640789724025921 03420001087906666634482930821819658694501159578269 80964984966314032404451971610123340406741635964361 36401216951748750742995259964669942373138603511253 63368100448195341951443958240072308018094787558167 20268950710383905924345191799770104935929423157322 35892479088630132854982514754473035710645823020846 2357632